Speeding up the GPT - KV cache
The common optimization trick for speeding up transformer inference is KV caching 1 2. This technique is so prominent that huggingface library has use_cache flag is enabled by default 6. A few days ago, I read an awesome blog post on GPT in 60 Lines of NumPy. So, i thought, why not extend it to use the KV cache technique? So, let’s roll up our sleeves and start working on it. Before you read further, the blog assumes you have background on transformers; if you don't, then read this blog post. It’s awesome, and you will learn a lot from it.
First, let’s understand a few things about GPT code.
def gpt(inputs: list[int]) -> list[list[float]]:
# inputs has shape [n_seq]
# output has shape [n_seq, n_vocab]
output = # beep boop neural network magic
return output
We can deduce from the input-output signature that we can provide arbitrary long input and receive output of the same length, with each element of the output indicating the probability of the next token. So, I can just give a single token as input and get the probability of next token. It should just work, right ?
Modifying the code of picoGPT to just give the input of the last single token and get the probability of the next token.
for _ in tqdm(range(n_tokens_to_generate), "generating"): # auto-regressive decode loop
logits = gpt2(inputs[-1:], **params, n_head=n_head) # model forward pass
next_id = np.argmax(logits[-1]) # greedy sampling
inputs = np.append(inputs, [next_id]) # append prediction to input
We are providing inputs[-1:] as input (single token) to the model. So, we are just passing a single token as input. Let's see what happens.
the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the
I didn’t work. Because the main magic is in the attention, in order to have good prediction of next tokens we need to provide all previous tokens. Although in practice, we do have limited memory and compute which forces us to provide context upto last N tokens. for example, chagpt has context upto 4096. In summary, We can’t just pass a single token and get very good prediction of next token. This makes attention have quadratic complexity.
But, if we look at the architecture of GPT, we can see that we only interact with previous tokens in the attention block, all other layers, such as the embedding layer, the feed forward layer, the layer norm, etc., don’t care about previous tokens. So, what if we can cache the input of the attention block for all previous tokens and pass it during inference? We don’t have to pass all these tokens again and again. We can just pass the last token and get the probability of the next token.
The input of the attention block is q, k, v and mask. We can try to cache q, k, and v for all previous tokens. But, let’s think about what really matters for us. We only need k and v of the previous tokens to perform attention on the current input token because we are only passing one token as input. See the image below for a visual representation of what I mean.
def attention(q, k, v, mask): # [n_q, d_k], [n_k, d_k], [n_k, d_v], [n_q, n_k] -> [n_q, d_v]
return softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) @ v
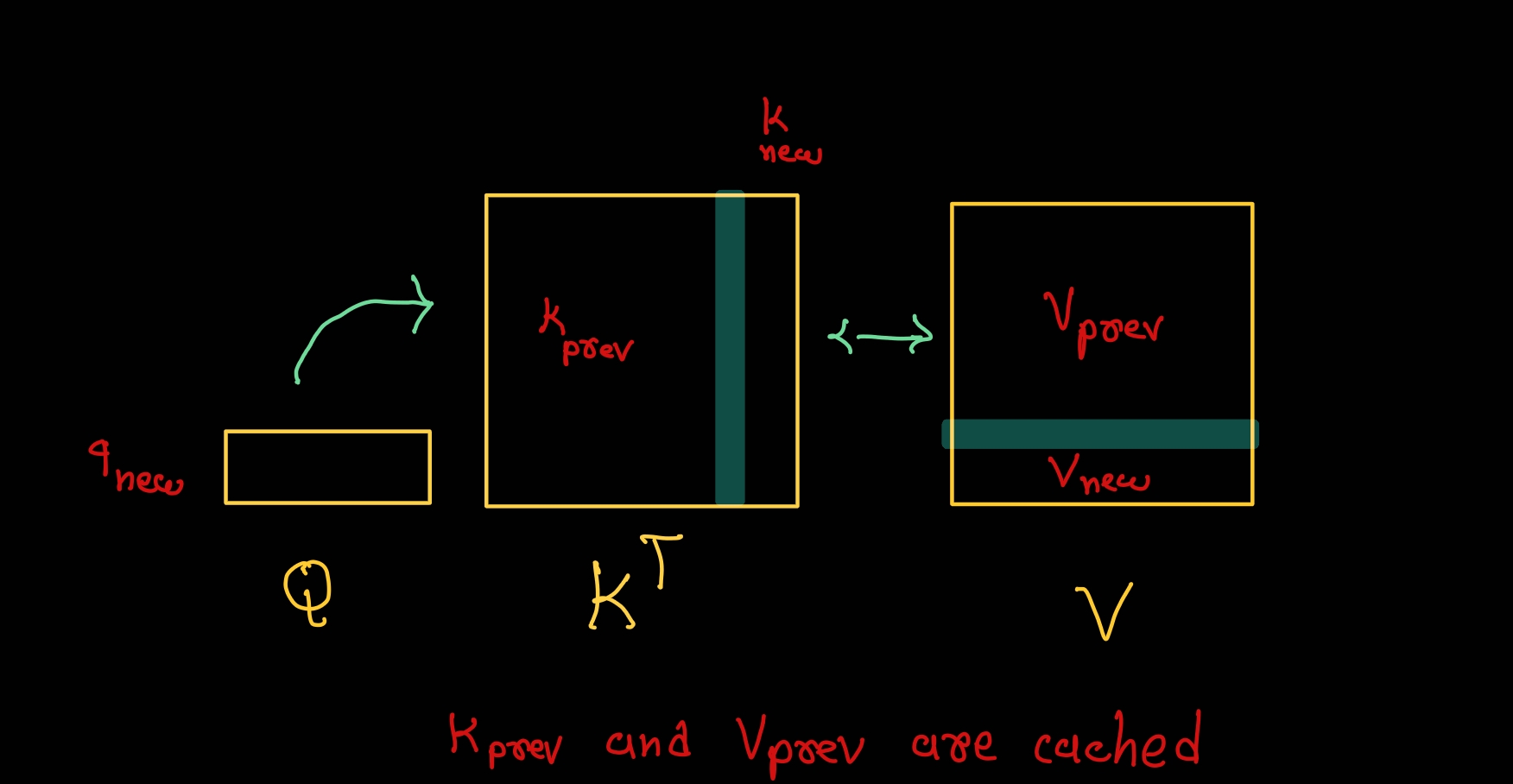
So, we need to calculate new_k and new_v for current input token. Append it to the existing cache and pass it to attention block for further processing.
def mha(x, c_attn, c_proj, n_head, kvcache=None): # [n_seq, n_embd] -> [n_seq, n_embd]
# qkv projection
# when we pass kvcache, n_seq = 1. so we will compute new_q, new_k and new_v
x = linear(x, **c_attn) # [n_seq, n_embd] -> [n_seq, 3*n_embd]
# split into qkv
qkv = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> [3, n_seq, n_embd]
if kvcache:
# qkv
new_q, new_k, new_v = qkv # new_q, new_k, new_v = [1, n_embd]
old_k, old_v = kvcache
k = np.vstack([old_k, new_k]) # k = [n_seq, n_embd], where n_seq = prev_n_seq + 1
v = np.vstack([old_v, new_v]) # v = [n_seq, n_embd], where n_seq = prev_n_seq + 1
qkv = [new_q, k, v]
There is one more thing we need to take care of is causal mask. When we pass single token we would like it to attend to all previous tokens.
# causal mask to hide future inputs from being attended to
if kvcache:
# when we pass kvcache, we are passing single token as input which need to attend to all previous tokens, so we create mask with all 0s
causal_mask = np.zeros((1, k.shape[0]))
else:
# create triangular causal mask
causal_mask = (1 - np.tri(x.shape[0])) * -1e10 # [n_seq, n_seq]
Combining all the things together, we get the following code.
def mha(x, c_attn, c_proj, n_head, kvcache=None): # [n_seq, n_embd] -> [n_seq, n_embd]
# qkv projection
# n_seq = 1 when we pass kvcache, so we will compute new_q, new_k and new_v
x = linear(x, **c_attn) # [n_seq, n_embd] -> [n_seq, 3*n_embd]
# split into qkv
qkv = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> [3, n_seq, n_embd]
if kvcache:
# qkv
new_q, new_k, new_v = qkv # new_q, new_k, new_v = [1, n_embd]
old_k, old_v = kvcache
k = np.vstack([old_k, new_k]) # k = [n_seq, n_embd], where n_seq = prev_n_seq + 1
v = np.vstack([old_v, new_v]) # v = [n_seq, n_embd], where n_seq = prev_n_seq + 1
qkv = [new_q, k, v]
current_cache = [qkv[1], qkv[2]]
# split into heads
qkv_heads = list(map(lambda x: np.split(x, n_head, axis=-1), qkv)) # [3, n_seq, n_embd] -> [n_head, 3, n_seq, n_embd/n_head]
# causal mask to hide future inputs from being attended to
if kvcache:
causal_mask = np.zeros((1, k.shape[0]))
else:
causal_mask = (1 - np.tri(x.shape[0])) * -1e10 # [n_seq, n_seq]
# perform attention over each head
out_heads = [attention(q, k, v, causal_mask) for q, k, v in zip(*qkv_heads)] # [n_head, 3, n_seq, n_embd/n_head] -> [n_head, n_seq, n_embd/n_head]
# merge heads
x = np.hstack(out_heads) # [n_head, n_seq, n_embd/n_head] -> [n_seq, n_embd]
# out projection
x = linear(x, **c_proj) # [n_seq, n_embd] -> [n_seq, n_embd]
return x, current_cache
We introduced minor breaking changes in output as well. We are introducing current_cache alongside our normal output. This is because we can use an updated cache for the next run.
We also need to change a few functions to make it work.
def transformer_block(x, mlp, attn, ln_1, ln_2, n_head, kvcache=None): # [n_seq, n_embd] -> [n_seq, n_embd]
# multi-head causal self attention
attn_out, kvcache_updated = mha(layer_norm(x, **ln_1), **attn, n_head=n_head, kvcache=kvcache)
x = x + attn_out # [n_seq, n_embd] -> [n_seq, n_embd]
# position-wise feed forward network
x = x + ffn(layer_norm(x, **ln_2), **mlp) # [n_seq, n_embd] -> [n_seq, n_embd]
return x, kvcache_updated
We added kvcache as an input to the function and returned kvcache_updated as an output for each transformer block. We also need to change transformer function.
def gpt2(inputs, wte, wpe, blocks, ln_f, n_head, kvcache = None): # [n_seq] -> [n_seq, n_vocab]
if not kvcache:
kvcache = [None]*len(blocks)
wpe_out = wpe[range(len(inputs))]
else: # cache already available, only send last token as input for predicting next token
wpe_out = wpe[[len(inputs)-1]]
inputs = [inputs[-1]]
# token + positional embeddings
x = wte[inputs] + wpe_out # [n_seq] -> [n_seq, n_embd]
# forward pass through n_layer transformer blocks
new_kvcache = []
for block, kvcache_block in zip(blocks, kvcache):
x, updated_cache = transformer_block(x, **block, n_head=n_head, kvcache=kvcache_block) # [n_seq, n_embd] -> [n_seq, n_embd]
new_kvcache.append(updated_cache) # TODO: inplace extend new cache instead of re-saving whole
# projection to vocab
x = layer_norm(x, **ln_f) # [n_seq, n_embd] -> [n_seq, n_embd]
return x @ wte.T, new_kvcache # [n_seq, n_embd] -> [n_seq, n_vocab]
Notice, When we have already compute kvcache, we only return input last token to GPT2 alongside with kvcache. You can also see len(kvcache) == # number of transformer blocks. This is because we need to update kvcache for attention and we have single attention in each transformer block.
And, finally, it's time to change our generate function to use cache. In the first iteration, we will not have kvcache and we will pass kvcache=None to gpt2 function. In subsequent iterations, we will utilise the previously generated kvcache.
kvcache = None
for _ in tqdm(range(n_tokens_to_generate), "generating"): # auto-regressive decode loop
logits, kvcache = gpt2(inputs, **params, n_head=n_head, kvcache=kvcache) # model forward pass
next_id = np.argmax(logits[-1]) # greedy sampling
inputs = np.append(inputs, [next_id]) # append prediction to input
This cache helps us to reduce computation for each iteration. We can see that, in first iteration, we are computing attention for all tokens in input. But, in subsequent iterations, we are only computing attention for last token. Reducing time complexity from O(n^2) to O(n).
Finally, we can verify generate text with our previous code which didn't have caching and compare two output. Both output should be same.
In terminal
>>> python gpt2_kvcache.py "Alan Turing theorized that computers would one day become"
Output:
the most powerful machines on the planet.
The computer is a machine that can perform complex calculations, and it can perform these calculations in a way that is very similar to the human brain.
You can see the all the code in this pull request. You can also see the code in this repository.
You can see more details of calculation related to kv cache memory footprint calculation and computation time in this blog post.
References: